CA Motorcycle Accident Statistics: Don't Ride at Night

Motorcycles are generally considered to be a dangerous form of transportation. Plenty of sources publish basic statistics to reinforce this idea, like the fact that even though the base rate of motorcycle accidents per registered motorcycle is about the same as that of cars ¹, approximately 80% of motorcycle accidents result in injury or death (compared with ~20% of car accidents)².

However, these sources rarely answer questions like:

• Which factors are the best predictors for motorcycle accidents or deaths?
• Does one type of unsafe operator behavior (like riding without a helmet) predict additional types of unsafe operator behavior?

These are the types of questions I was hoping to answer in this analysis.

The data set I used for this investigation was the California Highway Patrol Statewide Integration Traffic Reports System (SWITRS)³. This data set was readily available and large (constituting some 7 million collisions over 14 years), which avoided the usual "find the data" problem. On the other hand, this data was challenging to work with, because it included a complicated mishmash of possible features (with varying levels of data completeness, many of which were categorical), and it wasn't particularly tidy (records appeared to be entered as-is from traffic reports hand-coded by many idiosyncratic users, without much or any data validation). As such, most of my time on this project was spent cleaning data, validating data, and thinking critically about feature engineering.

The SWIRTS includes information about all collisions for all vehicles statewide, as well as all the parties involved in the collisions. So to look at motorcycles in particular, I joined the party dataset to the collisions dataset, and then filtered to include only the records where the vehicle in question was a motorcycle and the party in question was the driver. (As there's usually more than one party involved in a collision, this ensured there was only one record per collision, focused on the operator of the motorcycle). I mention this because it defines what we can and can't conclude based on this analysis. For example, my analysis can't describe anything about the safety of motorcycle passengers, and can't conclude anything about the behavior of the non-motorcycle drivers involved in a collision. All of this analysis is going to be conditional on "has been involved in an accident"; that is, we can't conclude anything about whether certain factors make it more or less likely to be in an accident. We can only conclude that, given that someone is already in an accident, certain features predict others. This is a fundamental limitation of this type of dataset, and it'll come up again later on. 

Motorcycle Fatalities

As mentioned, I was interested in investigating both predictors of fatalities as well as predictors of unsafe behavior. My procedure for the two investigations was very similar, so I'll walk through it for the "fatalities" model and then simply present conclusions for the "unsafe behaviors" model.

Before doing any modeling, I dummy-coded the categorical variables, and then created a matrix of correlation coefficients to get an initial feel for the data.  I like running correlation coefficients because it allows me (among other things) to keep an eye on features that are likely to be strong and useful predictors, to pinpoint features that don't seem very useful, and to identify and exclude useless inter-associations that might throw off my model (for example, "number injured in collision" and "number killed in collision" are very strongly associated, but that doesn't tell you much of substance - just that bad accidents are bad). Of course, correlation coefficients are only looking at linear relationships, so there's a lot they can miss, but they make a good first pass. Fatalities came out highly correlated with

• the age of the motorcycle driver
• riding under the influence of drugs, and
• the involvement of alcohol.

Unfortunately, while the SWIRTS includes fields for "violation category" (like unsafe speed, reckless driving, improper passing), it became clear at this stage that these were unlikely to be useful features due to inconsistent data entry. 

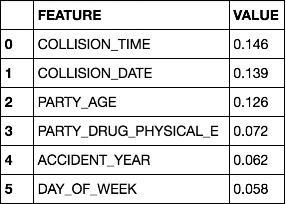
For my initial models, I ran straightforward random forest classifiers from scikitlearn. I've had good results in the past with this module for this size and type of data, and since I was primarily focused on identifying important factors (rather than very fine-tuned quantitative predictions) I wanted something where I could easily see feature importances, without complexity overkill. I split the data into train, test, and holdout sets, since there was plenty to go around. This model achieved 97% accuracy on the holdout set. Top feature importances were as follows: 

(where 'PARTY_DRUG_PHYSICAL_E' = under influence of drugs)

When I saw this, I was a bit suspicious - collision time, collision date, and party age all happen to be the features in the dataset with the highest number of bins. Scikitlearn's random forest classifier feature importance calculation is based on the Gini importance, which is biased towards high-cardinality variables.⁴ To resolve this, I first asked myself whether I actually needed such finely-scaled data in those variables. I decided that I definitely didn't for collision time, and replaced it with a 24-bin "collision hour" feature. Most of the information in "collision date" was also in "accident year", which was already in the analysis, so I threw out "collision date" entirely. I then reran the model, and the top feature importances order changed to:

I still wasn't fully satisfied (party age and hour still were the features with the most bins), so I implemented a second workaround to feature importances being potentially biased in this way - which is to drop the feature entirely, retrain the model, and observe the drop in accuracy or other performance measures compared with the original model resulting from the missing feature. While the feature-dropped models resulted in only negligible drops in accuracy, the precision and recall scores tell a different story: 

Both age-dropped and hour-dropped models resulted in a definite drop in precision, so they're both still important. (You might notice that the hour-dropped model performed even worse comparatively than the age-dropped one, despite being ranked as a less-important feature: age has about three times as many bins, so evidence for exactly the feature importance bias I was concerned about.) 

Speaking of precision and recall!

While the overall accuracy looks excellent, that recall is pretty poor for the "fatalities" class. In a case like this one, where we have many records but only a few of them result in fatalities, this points to a class imbalance problem. The model is leveraging the fact that fatalities only pop up 3.5% of the time, so in theory if it only ever predicted "no fatality", it'd be right 96.5% of the time. (It's not quite that bad in practice - this model is predicting fatalities about 1.5% of the time.) There are a few ways to deal with this, but a simple method is to undersample the majority class in the training set (another is "use a random forest", but we already did that). Undersampling can cause reduced model power (due to discarding some of our data), but this data set is large, and again: we're looking at factor importance here, not necessarily "most powerfully quantitative predictive model." So I went with an undersampled 50-50 class split as a good place to start, and the precision and recall scores changed as follows:

This is much more evenhanded, and I was satisfied for the time being. The most important features predicting fatalities were party age, the hour of the day, the day of the week, drug intoxication, and alcohol intoxication. 

The hour of day relationship is particularly striking:

We can see fatalities are much more likely to occur at night. There's a couple dips that suspiciously correlate with rush hour - perhaps there's more vehicles on the road, but the average driver is safer? Also, we can definitely see why this didn't pop up in the correlation coefficients matrix: this definitely isn't a linear relationship.

The age vs. fatality-likelihood relationship might not be what you were expecting: 

General wisdom says something like "young people are more reckless and have less experience operating a vehicle", so maybe we'd expect them to be more likely to die in an accident. My interpretation of this is we're looking at the importance of that conditional "given an accident has already occurred" that I mentioned earlier. It may be that young people get in more accidents, or it may not - we can't tell that one way or another from this data set. But this relationship shows a slow and steady increase in the likelihood of dying, conditional on already having gotten in an accident, as age increases (the error bars on the top end tell us that the bit where it gets all weird isn't too reliable, because there isn't enough data in those age bins). 

Fatalities are notably more likely on the weekends. This checks out with other sources' analysis on the same topic:⁵

1 = Monday. 6 and 7 are Saturday and Sunday.

The relationship between alcohol and fatalities was an interesting one.

 Although alcohol didn't show up particularly high in the feature rankings - a far distant fifth - it's quite clear from these averages that when alcohol is involved, fatalities are more likely. My best guess is this is because of its relative scarcity in the dataset: it's only present in about 8.5% of the samples. Perhaps it's important when it appears, but it appears so infrequently that the signal gets drowned out by other predictors. This is a good cautionary example about using data models - created to answer a specific question - like "what combination of features best predicts an outcome such as fatalities" - to answer different, more everyday behavioral questions - like "is it a good idea to drink and drive". (I have a whole post about something related, here.)

Unsafe Behaviors

This model went through essentially all the same steps as my fatalities model, described above, so I'll just share the conclusions. The goal of this model was to see if unsafe behaviors in the collisions dataset would predict other unsafe behaviors - I used "not wearing a helmet" as the target variable. In essence, do operators engaging in unsafe behavior tend to engage in other unsafe behaviors at the same time?  This model's predictive power suffered a bit from less data - unlike fatalities, the "unsafe behaviors" features were relatively inconsistently coded, and had a much bigger class imbalance problem.  The class-balanced model was hitting about 66% accuracy, recall 72% and 60% for "helmet" and "no helmet" classes, respectively. Some room for future improvement here, for sure.

The top feature importances predicting not wearing a helmet were age (by a significant margin!), hour of the day, day of the week, and alcohol involvement. Here's a visualization of age versus the likelihood of a fatality in the dataset:

Teenagers extremely less likely to wear a helmet. Do note that the legal driving age for motorcycles in California is 16. 

The hour-of-day relationship is very similar to the fatalities relationship, except with a much more pronounced dip for morning rush hour and less pronounced for evening:

People who drive late at night don't seem to wear helmets as often.

The day of the week relationship is also similar to fatalities, although less pronounced overall:

Riders are less likely to wear helmets on weekends.

Not wearing a helmet is associated with higher likelihood of alcohol involvement in the crash:

...despite alcohol involvement not being a particularly highly-ranked feature in my models. The reasons for this are likely similar to those for the fatalities models, discussed above.

Even citations for unsafe speed were associated with not wearing a helmet, despite not being even remotely highly ranked as a feature: 

There was very little data for this feature, so this is a more low-confidence result. A pattern does seem to be emerging, though, that the "unsafe operator behaviors" are inter-related. 

This post presents only a fraction of my work with this data set (otherwise it'd take days to read) and there's lots more yet to be done! I plan to publish a Part 2 at some point soon. The first expansion of this analysis will be to look more in-depth at only the records for which the motorcycle drivers were at fault (I had skimmed the correlation coefficients and didn't see anything that stuck out as terribly different, so I deprioritized it in my workflow). Running a PCA or similar dimension reduction for the "do unsafe behaviors cluster together" question might be interesting. After that, more model tuning, especially with different methods of class balancing: I definitely want to see what the imbalanced-learn library can do here. 

---

1. National Highway Traffic Safety Administration
2. Insurance Institute for Highway Safety
3. Available at http://iswitrs.chp.ca.gov/Reports/jsp/CollisionReports.jsp. Yes, it is "Statewide" instead of "State-Wide" like the acronym. No, I don't know why.
4. see e.g. http://explained.ai/rf-importance/index.html#2
5. e.g. Insurance Institute for Highway Safety, again

Creating Imaginary People with Statistics

A neat set of graphs was circulating on social media, called "The Effect of Life Events on Life Satisfaction". 

I was curious about the methodology, so I dug into the source, and discovered that there are two open-source versions of this paper. Uniquely, the 2006 version is an earlier version, and provides a cool opportunity to look at these graphs in both raw data and post-analysis form. 

It's a great case study for analyzing confounding/lurking variables carefully, and thinking critically about the real-life interpretations of those variables. 

Here's briefly how the analysis worked. The authors used a large longitudinal dataset that included a self-reported "life satisfaction" score for participants, as well as data on various life events the participants were experiencing. They looked at life satisfaction after the event/event onset ("lags") and leading up to the event ("leads").  The 2006 paper shows graphs for the raw happiness scores of their first analysis, in which they controlled only for "fixed" effects (essentially, accounting for the fact that happy people may self-select into happier life events, and vice versa). The 2007/8 paper shows the graphs from the stand-alone graphic, from their second analysis - a multivariate regression, which aimed to isolate the effects of a wide variety of potentially confounding variables (e.g. personal health problems, age, other major life events). That unlabelled Y-axis is the coefficient on the regression variable.    

Here's where comparing these graphs tells some interesting stories about lurking variables.

If you look at the raw 2006 data, widow(er)s look happier before their spouse's death (predictably), and that happiness recovers somewhat several years out, but not completely:

However, when they run the regression analysis and control for education, nationality, # of children, age, household income, individual health concerns, marriage state, and employment, that effect goes away, and if anything, the participants end up looking happier afterwards:

Since all the variables were controlled for at once and we don't have access to the raw data, we can't tell exactly what happened here - but clearly, one or more of those lurking variables are responsible for lower self-reported happiness after the death of a partner than could be predicted by death of a partner alone. Some non-inclusive possibilities:

• Children, being an additional burden to care for alone
• Loss of a second source of income leading to cash flow problems
• New health concerns

So this raises the question, when we remove these variables from the picture, how much does the remaining analysis reflect any situation in reality? When we ask a research question like "how much does widowhood affect happiness," if that widowhood often leads to secondary happiness-affecting issues like sudden single parenthood, loss of household income, etc., is it truly appropriate to remove those variables from the picture?

For a clearer example, let's look at layoffs:

These two graphs look very different, and when we look at the fine print, we discover that one of the things the second one is controlling for is income! So it's a realistic portrayal of... all those layoffs that don't result in a drop in income. (Ever had one of those? Me neither.) 

Now, to be fair, the authors did this on purpose: they were curious about the psychological effects of e.g. layoffs independent of the income effect. These graphs don't describe aggregated people in real-world situations, they describe vacuum effects. However, when these graphs escape from their original context into social media and the world at large, suddenly people are looking at them to answer a different question: "If I get laid off tomorrow, how will I feel in three years?" Now they're being interpreted as aggregated people. But they're people that don't (or rarely) exist: all those people that get laid off without losing income, or whose spouses die with no secondary effects whatsoever. It's a cautionary tale about statistics out of context.

Regression Modeling on a Groundwater Chemical Spill

Sometimes chemical contaminants get into groundwater aquifers. We want to get them out. In order to get them out, we have to know where they are in the aquifer - which, of course, is dozens to hundreds of feet underground and obscured from view. So we take samples. But every sample is expensive, time- and labor-intensive, and often involves lugging to remote areas machinery that looks like this:

CC BY-SA 3.0, https://en.wikipedia.org/w/index.php?curid=5434651

So what if you could take a small number of samples and then tentatively predict where the plume is - and perhaps where else you had to sample to make your prediction better - purely statistically?

I was very lucky to come across a publicly available contaminant plume full dataset; these are usually proprietary. This one is at the Massachusetts Military Academy, and it's an old wastewater plume. Here is a map of the site, directly from the journal publishing the case, with the sampling locations indicated as black dots and the approximate plume boundaries in yellow:

(Savoie et al., 2012)

The data came to me as three tables - well construction data (including coordinates and depth), organic contaminants, and inorganic contaminants, which all had to be cleaned and joined on well location. (Handy reminder: mixing decimal degrees with lat/long DMS can really mess up your maps!) According to the journal article, this plume was characterized primarily by high nitrate levels with some chloride and boron, so I picked nitrate concentrations as a first-pass target variable.  Since the goal is to predict neighboring sampling locations' nitrate concentrations, my initial features were the spatial coordinates. 

When we visualize the distribution of the target variable, we get something that looks like this:

...does that make you nervous? It makes me nervous!

The data ranges over three orders of magnitude, with a very heavy tail. Environmental contamination data sets are notorious for this kind of distribution and variability: from a common-sense standpoint, most samples are going to be low-contamination, but occasionally they will be very high, and it's important when they are.

 We can probably anticipate that this will cause problems in our model, which it did. More on that later.

The other major challenge in this data set is its relatively small size. Unfortunately, this is par for the course for groundwater data (see previous picture of giant drilling rig, and the underlying driver for this analysis in the first place). In fact, this data set is pretty comprehensive compared to your average groundwater data set, especially publicly-available. So "get a larger data set" isn't really an option for this kind of environmental data - any machine learning solutions for problems in this field are simply going to have to take this challenge into account. I knew overfitting was going to be a major concern for this data, and I didn't have a ton to spare for validation+holdout. I split off a 30% section to use for testing, and trained/cross-validated on the remainder.  

The first model I attempted was a Gaussian process regression (hereafter, GPR) implemented with scikit-learn's GaussianProcessRegressor. I picked this to start because of the attractive possibility of training on a comparatively sparse data set in order to return not only a model fit, but areas of highest uncertainty (which GPRs return easily): perhaps to inform future environmental sampling at the same remediation site. It's easy to conceptualize the GPR as trying to model an underlying mathematical process generating noisy data, which seemed like a good conceptual fit for our situation of a spreading plume (tidy math) being sampled in a real-world situation (messy reality). I spent a lot of time tuning this model. I tested RBF and exponential kernels head-to-head¹, and tuned parameters (mostly the white noise kernel contribution; in theory, the sklearn implementation automatically optimizes GPR hyperparameters during the model runs) to maximize test set predictive accuracy. Here is a 3-dimensional (rotate- and zoom-able!) spatial visualization of the predicted plume concentrations in the best model run:

Sanity-checking this, in a relatively homogeneous medium we would expect the highest concentrations to be found 1) near the surface towards the upgradient side in the direction of travel; and 2) in the center of the plume (midpoint) perpendicular to the direction of travel, tapering off towards the edges of the plume. By rotating the visualization above, we can see this appears to be generally the case, so it's got the right idea. However, the presence of a few random low-concentration points scattered throughout, along with the overall narrow range of predicted concentrations compared to the data set, are definitely reflective of the difficulty of training on such a small, high-variability dataset. More problematically, although accuracy scores aren't the beginning and end of the story, the test set R² accuracy score of this model was pretty bad. So I went back to feature engineering, and gave that nitrate distribution more scrutiny.

"Data that ranges over several orders of magnitude and looks skewed towards the left side of the distribution" makes me think log-normal, so I tried using log(nitrate) instead.² That looked a lot more promising:

We've still got the problem of a lot of observations at zero, but at least the long-tail issue has resolved. Re-running the model taking this into account increased the R² accuracy from ~0.01 to ~0.20, a huge improvement for a tough data set.

I still wasn't too happy with the performance of the GPR implementation I was using, so I switched models entirely to a random forest regressor, just to see how much more performance could theoretically be improved. It did incredibly well: R² = 0.5, and just in case I thought that accuracy score could be misleading, here are the visualizations of the model-predicted log(nitrate) concentrations compared to ground truth data:

I was happy enough with these results for the time being. For future work with this data set, I'd like to train a GPR iteratively, with the next sample being at the point of maximum predicted uncertainty, to determine whether this is a productive strategy for minimizing number of sampling points while maintaining reasonable model accuracy. I'd also like to see whether adding "neighboring concentrations of other contaminants" (boron, or chloride) as features is helpful for predicting target variable concentrations.³

---

[1] The idea here was that the exponential kernel is the theoretically correct choice for describing the covariance of a contaminant plume spreading according to the fractional advection-dispersion equation; research indicates that contaminant plumes spreading in predominantly-sand aquifers like the one underlying the Mass Military Academy exhibit super-Fickian behavior. Regardless of the potential cause, my exponential kernel did perform much better than the RBF kernel.

[2] It also turns out a lot of environmental data is log-normal, but we can derive this by examining the data, even if we didn't know that fact ahead of time. 

[3] And if someone who knows more about the GPR implementation in sklearn wants to help me make mine better, I'd be very excited! Documentation and internet-crowdsourced info for this implementation is minimal. 

Can Fish Selenium Concentrations be Predicted From USDA Nutrition Label Information?

As you're likely already aware, mercury content in seafood is a growing concern. Eating fish is probably good for you. Eating mercury is probably bad for you. What's an informed consumer who really likes tuna to do? 

The other day, I was reading up on the argument in the academic literature about selenium concentrations(that's the element, not the browser automation) in seafood being a protective factor against potential mercury toxicity from consuming the seafood. Of course, the standard approach is to avoid or reduce consumption of fish known to have high mercury content. But in general, telling people not to eat something they think is tasty is often a hard sell. The selenium idea comes in under the principle of "harm reduction": if you can't convince someone to give up swordfish AND tuna AND mackerel, maybe you can convince them to stick with the tuna if it shows higher protective selenium. It increases options. Anyway, some studies show a benefit; others, not. Yet others indicate there's a relationship, but the effect is more complicated. In any case, it seems like dietary selenium concentration might be something that a consumer of fish might be interested in being able to make informed choices about. Unfortunately, when our consumer buys a product at the store with a nutrition label on it, at best it's going to look something like this:

e.g. Alaska's Best Salmon Jerky. No endorsement, either for or against this product, is intended

The USDA regulates the information contained on nutrition labels, mandating that certain things be included. Selenium concentration is not one of those things. However! We have all of this other data. Perhaps we could use it.

The question I was trying to answer was, is there a simple, easily-useable statistical model or equation that could be applied to this data by a hurried consumer trying to get home to a healthy dinner? There isn't much point in an incredibly complicated model for this - maybe as proof of concept, but at that point, you might as well just look it up. The obvious candidate here is a regression model. 

I wrote a script to scrape all the entries in the "seafood" category from nutritionvalue.org, which sources from the USDA, for selenium concentration as well as 11 common nutrition label entries. Those were protein; Vitamins A, C, and D; Iron; Sodium; Potassium; Calcium; saturated fatty acids (SFA); and poly- and monounsaturated fatty acids (PUFA, MUFA) for good measure. I took a look at the data, and graphed out a few of the variable correlations (all normalized). Some of them are kind of neat. As expected (some nice data validation), all of the fatty acids correlate pretty heavily.

You can see which vitamins/minerals are fat soluble and which ones aren't. Vitamin D, for example, is, while Potassium is not:

There are some things that look vaguely correlated with Selenium, which we should take a closer look at:

The correlation coefficient table shows the largest correlations with Selenium to be Protein, at 0.23, and Iron, at 0.16. Potassium trails at 0.08. 

I used scikitlearn's LinearRegression to start, and created a first-pass model with an R² of 0.1 upon k-fold cross-validation. Not to be deterred, I tried a couple pipelines with PolynomialFeatures and the regression. They were either terribly overfit or still low-accuracy. I tried picking and choosing the features, running a model with only the promising-looking high correlation coefficient candidates. Still no dice. At this point, I switched tactics: I decided to try a random forest regression, even though it didn't fit the criteria of the model I was looking for, just to get a sense for what I could theoretically hope for with my regressions.

I ran a few random forests in different configurations, and the best cross-validated accuracy score I could manage was about 0.3. Iron, protein, and occasionally potassium came up as important features across several versions of the model; Vitamins C and D were usually unimportant.

So at this point, I think it's fair to take away that there isn't much predictive ability for selenium with these particular features in this data set. This makes sense from a biochemical standpoint; unlike (for example) the fatty acids, there aren't many other compounds in the data set with similar chemical properties to selenium. I could sit here and grasp at straws to try and spin this model to have positive results, but no one learns anything from that. In fact, I think that demonstrating negative results is important and worthwhile! We now have some support to say something like, "This is information missing from these labels, for which there aren't great proxies. Consumers who care about knowing this information should lobby the USDA for its inclusion." 

I don't think I'm entirely done with this dataset. The next step for this project is going to be joining the data with a mercury concentrations dataset, to see if any interesting conclusions (selenium or otherwise) can be drawn about food safety and informed consumer decision-making. 

Just for fun, I'll close with this table of the top 10 highest selenium concentrations in the database, so you can make your own informed seafood-purchasing decisions!

Minipost: Considerations for "Small" Data Sets

Why might a data set be small?

We’d like to be up to our ears in all the data we want, all the time, but sometimes that just isn’t the case. This could be because you’re having trouble sourcing data, in which case you might want to work directly on that problem, but it could be for other reasons that are harder to work around. Maybe the thing you’re looking at is just naturally limited in size, like the number of different species of fish on the planet. Maybe your goals require deeper analysis of a very specific subset or slice of your data. You might be stuck with the data you have.

Common challenge areas

Overfitting

A powerful model can often quickly and easily overfit to every single point in your relatively small data set. Be on the lookout even more than usual for common signs of overfitting, be sure to properly cross-validate, and definitely consider using regularization terms.

More fundamentally, model selection can be key here- conceptually speaking, what is your hypothetical model suggesting about the underlying relationships in your data, and how well does that match your understanding of the context of the data and the processes that generated it?

Model cross-validation

You might not have enough data points for a train-test-holdout split to be a fruitful endeavor: either you’ll be lacking training data and end up with a poor model, or you’ll be lacking testing data and be unable to draw useful conclusions about model performance. K-fold cross-validation or Leave-one-out on your test data could be a better option.

Outliers

You don’t have the leeway to be careless with outlier removal. One one side, inappropriately including outliers in a small data set could skew your model in a major way. On the other, being too conservative could result in too many data points being excluded, which will have a large impact on the statistical power of your model. Thinking critically about the conceptual underpinnings of the outliers in your data set can be helpful.

Minipost: Handling Nondetects and Missing Data

In general, there are three types of ways to deal with nondetects and missing data:

1. Drop the whole observation with the missing data

2. Use some statistical method designed for dealing with missing data

3. Impute the missing values, either with a single value or by using a model

In order to decide which method is best to use, it’s important to think carefully about a few things.

Most importantly, are your data systematically missing in some way? For example, are you looking at crime data for neighborhoods, and all the high-crime neighborhoods are underreported? Systematically missing data can cause major problems, so it’s important to rule out possible sources of systematically missing data as much as you can.

How much data are you missing? 0.5%? 20%? Different methods are more or less successful depending on the percentage of missing data.

What is the real-world meaning of the data set you’re studying, and what are the possible sources of missing data? Let the type of data you’re using, its purpose, and its structure inform the strategies you use.

Finally, what are the potential consequences if missing data is handled incorrectly? Are imputed values going to be problematic in some way, and how does that balance against the possibility of reduced statistical power in the analysis?

It’s easy to look up particular methods, but one thing you can’t just look up is how to think critically about the most intelligent ways to handle your missing data. Not all data sets can be treated the same.

(Once you've thought through these things, check out one of my favorite Python packages, which helps you examining missing data - missingno.)